Given an integer array nums and an integer k, return true if nums has a good subarray or false otherwise.

A good subarray is a subarray where:

• its length is at least two, and
• the sum of the elements of the subarray is a multiple of k.

Note that:

• A subarray is a contiguous part of the array.
• An integer x is a multiple of k if there exists an integer n such that x = n * k. 0 is always a multiple of k.

Example 1:

Input: nums = [23,2,4,6,7], k = 6
Output: true
Explanation: [2, 4] is a continuous subarray of size 2 whose elements sum up to 6.

public boolean checkSubarraySum(int[] nums, int k) {
    Map<Integer, Integer> map = new HashMap<>(){{put(0,-1);}};;
    int runningSum = 0;
    for (int i=0;i<nums.length;i++) {
        runningSum += nums[i];
        if (k != 0) runningSum %= k; 
        Integer prev = map.get(runningSum);
        if (prev != null) {
            if (i - prev > 1) return true;
        }
        else map.put(runningSum, i);
    }
    return false;
}

let’s break down this code visually. The goal is to find if there’s a subarray (a continuous part of the array) whose elements sum up to a multiple of k.

The core idea relies on this mathematical property:

If the sum of elements from index 0 to i (let’s call it sum_i) and the sum of elements from index 0 to j (let’s call it sum_j), where j > i, have the same remainder when divided by k, then the sum of the subarray from i+1 to j must be a multiple of k.

Why? If sum_i % k == R and sum_j % k == R, Then (sum_j - sum_i) % k == (R - R) % k == 0. And sum_j - sum_i is exactly the sum of the elements in the subarray (i, j].

The code uses a HashMap to store the first time it sees a particular runningSum % k value.

Visual Explanation

Let’s trace the example: nums = [23, 2, 4, 6, 7] and k = 6.

Initial State:

• map = {0: -1} (We initialize with 0 pointing to -1. This handles cases where the subarray starting from index 0 is a multiple of k.)
• runningSum = 0

Iteration 1: i = 0, nums[0] = 23

1. runningSum += nums[0] => runningSum = 0 + 23 = 23
2. if (k != 0) runningSum %= k => runningSum = 23 % 6 = 5 [23, 2, 4, 6, 7] ^ runningSum = 23 runningSum % 6 = 5
3. Integer prev = map.get(runningSum) => prev = map.get(5) which is null (5 is not in the map yet).
4. else map.put(runningSum, i) => map.put(5, 0) map = {0: -1, 5: 0}

Iteration 2: i = 1, nums[1] = 2

1. runningSum += nums[1] => runningSum = 5 + 2 = 7 (Remember runningSum from the previous step was 5 after the modulo. The code actually adds to the full runningSum before the modulo, so it should be 23 + 2 = 25. Let’s correct that understanding for the runningSum variable itself. The key for the map is the modulo.) Corrected runningSum accumulation: runningSum = 23 (from previous full sum) runningSum += nums[1] => runningSum = 23 + 2 = 25
2. if (k != 0) runningSum %= k => currentModulo = 25 % 6 = 1 [23, 2, 4, 6, 7] ^ runningSum = 25 (23+2) currentModulo = 25 % 6 = 1
3. Integer prev = map.get(currentModulo) => prev = map.get(1) which is null.
4. else map.put(currentModulo, i) => map.put(1, 1) map = {0: -1, 5: 0, 1: 1}

Iteration 3: i = 2, nums[2] = 4

1. runningSum += nums[2] => runningSum = 25 + 4 = 29
2. if (k != 0) runningSum %= k => currentModulo = 29 % 6 = 5 [23, 2, 4, 6, 7] ^ runningSum = 29 (25+4) currentModulo = 29 % 6 = 5
3. Integer prev = map.get(currentModulo) => prev = map.get(5) which is 0.
4. if (prev != null) is true.
   • if (i - prev > 1) => if (2 - 0 > 1) => if (2 > 1) which is true.
   • return true;

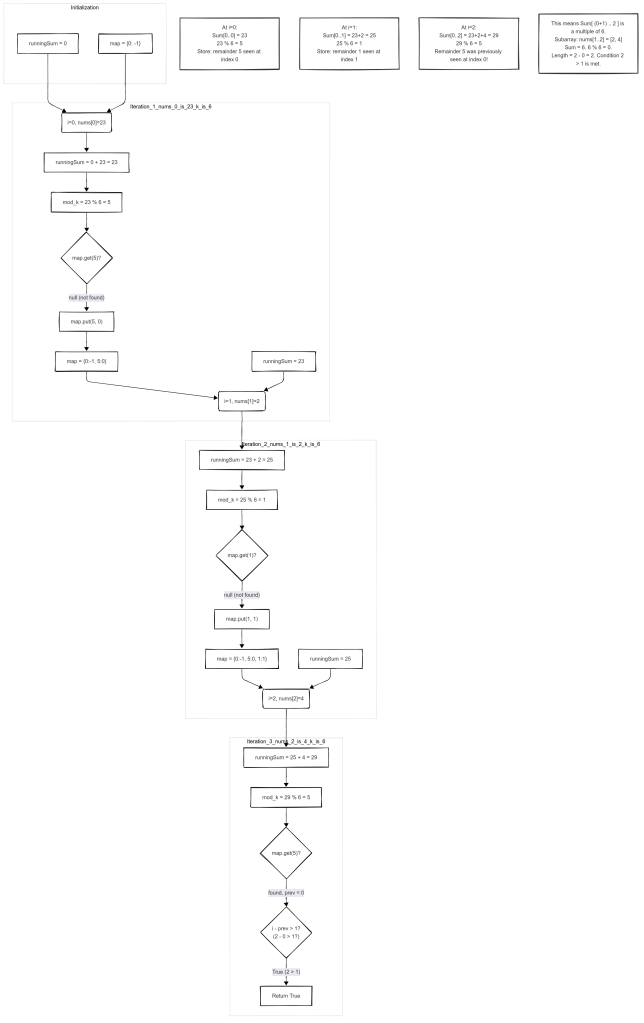
The diagram provides a flow. I think combining this with the table and the step-by

Visualizing the Process

Let’s use nums = [23, 2, 4, 6, 7] and k = 6.

Key Variables:

• runningSum: The sum of elements from nums[0] up to the current element.
• map: A dictionary (HashMap) that stores {remainder: index}. It’s initialized with {0: -1}. This special entry helps if a subarray starting from the very beginning (index 0) sums to a multiple of k. The -1 ensures that if the sum nums[0]...nums[i] is a multiple of k, the length i - (-1) = i + 1 is considered.
• i: The current index in the nums array.

Step-by-Step:

Initial State:

• runningSum = 0
• map = {0: -1}

Array: [23,  2,  4,  6,  7]
         ^
         i=0

1. i = 0, nums[0] = 23

• runningSum = 0 + 23 = 23
• remainder = runningSum % k = 23 % 6 = 5
• Is remainder (5) in map? No.
• Add remainder: i to map: map.put(5, 0)
• map is now {0: -1, 5: 0}

Visual: Sums: [23] Rem (k=6): [5] Map: {0:-1, 5:0}

Array: [23,  2,  4,  6,  7]
             ^
             i=1

2. i = 1, nums[1] = 2

• runningSum = 23 + 2 = 25 (This is the actual sum; the variable runningSum in the code stores runningSum % k if k is not 0, but it’s easier to think about the true sum first, then the modulo)
• The code does runningSum += nums[i], so if runningSum was 5 (from 23%6), it would become 5+2=7. Then 7%6 = 1.
• Let’s follow the code:
  • runningSum (from previous step, after modulo) = 5. (If k=0, this step is skipped)
  • runningSum (before adding nums[i]) is actually the full sum up to i-1. So, the code’s runningSum variable will accumulate the actual sum.
  • runningSum = 23 (full sum up to previous element)
  • runningSum += nums[1] => runningSum = 23 + 2 = 25
• remainder = runningSum % k = 25 % 6 = 1
• Is remainder (1) in map? No.
• Add remainder: i to map: map.put(1, 1)
• map is now {0: -1, 5: 0, 1: 1}

Visual: Sums: [23, 25] (sum up to index 0, sum up to index 1) Rem (k=6): [5, 1] Map: {0:-1, 5:0, 1:1}

Array: [23,  2,  4,  6,  7]
                 ^
                 i=2

3. i = 2, nums[2] = 4

• runningSum = 25 + 4 = 29
• remainder = runningSum % k = 29 % 6 = 5
• Is remainder (5) in map? Yes! map.get(5) gives prev = 0.
• Now, check the condition: if (i - prev > 1)
  • i = 2, prev = 0
  • 2 - 0 > 1 => 2 > 1. This is TRUE.
• Return true. We found a subarray!

Visual: Sums: [23, 25, 29] Rem (k=6): [ 5, 1, 5] <– We found a repeated remainder! Map: {0:-1, 5:0, 1:1}

Why did this work?

• At i = 2, the runningSum % 6 is 5. (Sum 23+2+4 = 29)
• We previously saw runningSum % 6 = 5 at prev = 0. (Sum 23)

This means the sum of elements between index prev (exclusive) and i (inclusive) is a multiple of k. Subarray: nums[prev + 1 ... i] => nums[0 + 1 ... 2] => nums[1 ... 2] Elements: [2, 4] Sum: 2 + 4 = 6 And 6 is a multiple of k=6. The length of this subarray is i - prev = 2 - 0 = 2. Since 2 > 1, the condition is met.

Diagrammatic Representation of the “Aha!” Moment:

nums:      [23,   2,   4,   6,   7]
index:      0     1    2    3    4

Running Sums:
S[0] = 23
S[1] = 23+2 = 25
S[2] = 23+2+4 = 29

Remainders (mod 6):
R[0] = 23 % 6 = 5  (Seen at index 0)  <--- Previous occurrence (prev_index = 0)
R[1] = 25 % 6 = 1  (Seen at index 1)
R[2] = 29 % 6 = 5  (Seen at index 2)  <--- Current occurrence (current_index = 2)

Since R[2] == R[0]:
The sum of the subarray (nums[prev_index + 1] ... nums[current_index]) is a multiple of k.
Subarray: nums[0+1 ... 2] = nums[1 ... 2] = [2, 4]
Sum = 2 + 4 = 6.
6 % 6 = 0 (it's a multiple!)

Length condition: current_index - prev_index > 1
                  2 - 0 > 1  =>  2 > 1 (True)

What if k = 0? If k is 0, the line runningSum %= k; is skipped. The map stores the actual runningSum values. If a runningSum repeats, it means the subarray between the two occurrences sums to 0. For example, if sum_j == sum_i, then sum_j - sum_i == 0. The condition i - prev > 1 still ensures the subarray has at least two elements.

The map.put(0, -1) explanation: This handles cases where a subarray starting from the beginning (index 0) sums to a multiple of k. Example: nums = [6, 1], k = 6

1. i = 0, nums[0] = 6.
   • runningSum = 6.
   • remainder = 6 % 6 = 0.
   • Is remainder (0) in map? Yes, map.get(0) gives prev = -1.
   • Check i - prev > 1: 0 - (-1) > 1 => 1 > 1. This is FALSE.
   • So, we don’t return true yet. (This is because [6] is a subarray of length 1, and the condition i - prev > 1 implies a length of at least 2 for the found subarray).
   • map.put(0, 0) (Now 0 maps to 0, overriding -1).
2. Loop continues or ends. If no other subarray is found, it returns false.

If nums = [2, 4], k = 6:

1. i = 0, nums[0] = 2. runningSum = 2. rem = 2. map = {0:-1, 2:0}.
2. i = 1, nums[1] = 4. runningSum = 2+4=6. rem = 0.
   • Is 0 in map? Yes, prev = map.get(0) which is -1.
   • Check i - prev > 1: 1 - (-1) > 1 => 2 > 1. This is TRUE.
   • Return true. The subarray nums[(-1)+1 ... 1] which is nums[0...1] (i.e., [2,4]) sums to 6. Length is 2.

The i - prev > 1 condition is crucial for ensuring the identified subarray has a length of at least two. If a subarray of length one (a single element being a multiple of k) was also a valid solution, the condition would be i - prev >= 1.